고정 헤더 영역
상세 컨텐츠
본문
- Quick Sort
평균적으로 볼 때 가장 좋은 성능인 O(nlogn)을 갖는 비교 기반 알고리즘이다.
특정한 킷값을 기준으로 주어진 입력 리스트의 원소를 적당히 이동시키면서 다음의 두 조건이 만족하도록 왼쪽과 오른쪽의 두 개의 서브리스트로 분할한다.
피벗(Pivot) : 퀵 정렬에서 리스트의 분할을 위한 특정한 키.
※ 대게 가장 왼쪽의 원소를 피벗으로 정함.
퀵 정렬의 핵심은 주어진 리스트를 피벗을 기준으로 두 개의 서브리스트로 분할하는 것이다.
※ 피벗이 제자리를 잡도록 하여 정렬하는 방식

1. L은 오른쪽으로 이동하며 R은 왼쪽으로 이동한다.
2. L은 피벗보다 작은 값이 위치하며, R은 피벗보다 큰값만 위치한다.
3. 만약 L > R 경우 L과 R값의 위치를 바꾸어 준다.
4. R의 인덱스값이 L보다 작을 경우 예) R[index] < L[index] R과 피벗을 바꾸어준다.
5. 1 cycle 종료,

Quick sort 분할정복 형식이다.
• 분할 : 정렬할 n개 원소를 피벗을 중심으로 두 개의 서브리스트로 분할한다.
• 정복 : 두 서브리스트에 대해 퀵 정렬을 각각 순환적으로 적용하여 두 서브리스트를 정렬한다.
• 결합 : 이 과정에서 결합은 필요 없다.
※ 리스트 분할 과정은 단순히 리스트의 크기에 비례하여 O(n)의 수행 시간을 갖는다.
서브리스트의 크기는 까지 다양하게 나올수 있다.
최선의 수행시간은 O(nlogn)이 된다.
※ 최악의 경우 : 피벗이 리스트에서 항상 최대값, 최소값이 되는 경우

- Merge sort
쪼갤 수 없을 때 까지 리스트 원소를 쪼갠다. 그리고 인접한 원소 간 비교하여 작은 값은 좌측 큰 값은 우측으로 정렬 한다.


합병 정렬(Merge Sort)의 분할정복 방법은 아래와 같다.
• 분할 : 정렬할 n개의 원소를 n/2의 원소를 갖는 두 서브리스트로 분할한다.
• 정복 : 두 서브리스트에 대해 합병 정렬을 각각 순환 적으로 적용하여 두 서브 리스트를 정렬한다.
• 결합 : 정렬된 두 서브리스트를 합병하여 원래의 정렬된 리스트를 만든다.
※ 평균 수행 시간모두 O(nlogn)이다.
탐색 알고리즘
원하는 데이터를 효율적으로 찾기위한 방법
1. 순차 탐색
- 리스트에 데이터가 연속적으로 저장되어 있는 경우 일반적으로 적용되는 방법이다.

크기가 n인 선형 리스트에서 순차 탐색의 최악의 시간복잡도는 O(n)이고, 평균 비교 횟수는 (n+1)/2가 되기 때문에 데이터의 양이 많은 경우 비효율적이다.
※ 단 입력이 리스트이지만 하면 언제라도 적용 가능한 탐색알고리즘이고, 데이터가 정렬되지 않은 경우에 적합하다.
2. 이진탐색
이진탐색은 주어진 데이터가 Key 값에 ㄸ라 미리 정렬되어 있는 경우에 적용할 수 있다.
• 탐색키 = 중앙원소값 → 탐색 성공
• 탐색키 > 중앙원소값 → 이진탐색(리스트 전반부, 우측)
• 탐색키 < 중앙원소값 → 이진탐색(리스트 후반부, 좌측)
탐색 되는 대상의 데이터 개수가 1/2 로 줄어들기 때문에 시간복잡도는 O(nlogn)이다.
※ 데이터가 정렬된 경우 우수한 성능을 보이지만, 삽입/삭제 연산과 같은 동적 연산이 많은 응용분야에는 적합하지 않다.

3. 이진 탐색 트리
이진탐색트리는 어떤 노드에 대해서도 다음의 두가지 성질을 만족하는 이진트리이다.
• 한 노드의 왼쪽 서브트리에 있는 모든 킷값은 그 노드의 Key 값보다 작다.
• 한 노드의 오른쪽 서브트리에 있는 모든 Key 값은 그 노드의 Key 값보다 크다.
3.1 탐색
루트에서부터 원하는 킷값을 갖는 원소를 찾아나가는 방식이다.

3.2 삽입
이진 탐색 트리에서 새로운 원소의 삽입은 삽입할 원소를 탐색하다가 비교할 노드가 없으면(탐색 실패한 경우) 그 위치에 새로운 노드를 삽입한다.

3.3 삭제
이진탐색 트리에서 원소의 삭제는 삭제할 원소를 탐색한 후 찾은 노드를 삭제하고 남은 노드들의 위치를 조절해주어야한다.
조절하기 위해선 이진트리의 성질에 만족하여야한다.
후속자 노드(Successor Node) : 어떤 노드의 바로 다음 킷값을 갖는 노드.

후속자 노드
7 → 15 → 22 → 30 → 35 → 40 → 44 → 55→ 88
7의 후속자 (Successor Node)는 15
15의 후속자(Successor Node)는 22
...
삭제되는 노드의 자식의 개수에 따라 다음과 같이 구분한다.
①. 자식이 없는 리프(Leaf)노드 일 경우 위치 조절이 필요 없다. 7, 22, 40, 88은 리프 노드이므로 그냥 삭제해주면 된다.
②. 자식이 하나만 있으면 자식노드를 삭제하고 노드의 위치를 위로 올리면 서브트리도 그냥 따라 올라오게 된다.
③ 자식이 두 개 모두 있다면, 후속자 노드를 삭제되는 노드의 위치로 올리면 서브트리도 따라 올라온다.
15를 지울 경우 15의 후속자 노드인 22를 위로 올리면 된다.
3.4 문제점
전체 노드의 개수가 n개 일 때, 탐색과정은 최대 logn번의 노드를 비교 하여 최선, 평균 탐색시간 O(logn)을 갖는다.
경사진 이진트리가 형성되면 최악의 탐색시간인 O(n)을 갖는다.
4. 해싱
해싱은 데이터의 키 값을 이용해서 데이터의 저장 장소를 계산하고, 이를 이용해서 데이터를 저장/탐색 하는 방법이다.
키가 주어지면 이에 대응되는 함수가 필요로하면 이를 해시함수(hash Function)이라고 한다,
충돌 : 서로 다른 키 값을 가진 데이터임에 불구하고 같은 저장주소에 대응되는 경우가 발생 하는 것
4.1 계산 잔여법(Division remainder hashing, modulo division)
저장 공간 크기를 m 이라할 때

※ m의 선택의 주의
• m에 따라서 해시 테이블의 크기가 자동으로 결정됨.
• 충돌 발생 가능성을 최소화 하도록 선점
- 해시 테이블의 크기보다 작은 소수로 선택하는 것이 바람직하다.
바람직한 해시 함수
• 계산이 용이 해야 한다.
• 각 키 값을 테이블의 각 슬롯에 균등하게 사상 시킬수 있어야함.
4.2 중간 제곱법
- 키 값은 제곱한 결과에서 중간 부분의 적당한 크기 자릿수를 취하는 방법

4.3 폴딩법
키 값 K 0001110111010000
① 중간으로 반으로 나눈다.
00011101 11010000
② 연산을 한다. (예 덧셈, XOR , AND)
00011101
11010000
ADD -----------
11101101 → 237 연산된 곳을 주소로 사용한다.
4.4 기수 변환법
• 어떤 진법으로 표현된 키를 다른 진법으로 표현 된다고 간주하고 키를 변환하는 방법

1370 주소값에 저장
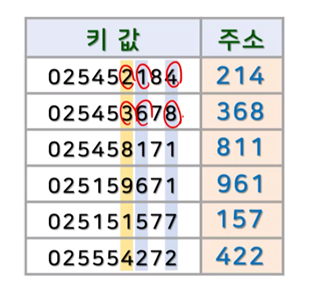
4.5 자릿수 추출법
- 키 가 취할수 있는 모든 키 값들에게서 그 키를 구성하는 자릿수들의 분포를 조사하여 비교적고른 분포로 보이는 자릿수 들을 필요한 만큼 택하는 방법
① 모든 킷값을 알고 있는 경우 에만 사용
② 빈번한 삽입 삭제의 경우에는 킷값 분포를 다시 조사해야 하기 때문에 비효율적
- 충돌 해결법
연쇄법 : 데이터들을 연결리스트를 사용하여 연결시키는 방법
개방주소법 : 충돌이 발생하면 새로운 데이터를 위치 할 수 있는 빈 공간을 찾는 것
선형 탐사법, 이차형 탐사, 이중 해싱 이 있다.
① 선형 탐사법
충돌이 발생한 인덱스와 인접한 다음 인덱스에 빈 공간에 데이터를 저장하는 방법
※ 1차 클러스터링 문제가 발생
클러스터링 문제 : 점유된 위치가 연속적으로 나타내어 탐색속도를 느리게 하여 발생하는 성능저하 문제
② 이차형 탐사
충돌이 발생한다면 빈 공간을 찾기위해 2차원 함수를 사용하여 빈공간을 계산한다.
※ 2차 클러스터링 문제 발생한다.
③ 이중 해시
충돌이 발생하였을 때, 또 다른 해시 함수를 사용하여 두 번째 이후 탐사 위치를 결정하여 첫 번째탐사 위치와 독립성을 이룬다.
'Tips > 대학' 카테고리의 다른 글
| 알고리즘 -1 삽입정렬, 버블정렬, 선택정렬 (0) | 2019.10.15 |
|---|---|
| 가계 재무관리를 위한 기초개념 (0) | 2019.10.13 |
| 컴퓨터 과학 개론 - 자료구조 스택, 큐 , 그래프 (0) | 2019.10.10 |
| 컴퓨터과학개론 -자료구조, 선형리스트, 연결리스트 (0) | 2019.10.02 |
| 언어의 이해-언어학은 무엇을 연구하는가? (0) | 2019.09.30 |
| 언어의 이해 -언어란 무엇인가. (0) | 2019.09.29 |




